Maths & TICE ! Algorithmes et Technologies de l'Information et de la Communication pour l'Enseignement
Sur cette page, des algorithmes, des scripts Python, des exemples Scratch, des modèles Géogébra, ...
Pour tester vos algorithmes, Algobox : ici.
Pour développer vos magnifiques programmes, Thonny, un excellent éditeur Python : ici. Et une carte mentale très résumée : ici.
Un parcours de formation : ici
Le lien vers Géogébra : ici.
Pour installer Scratch : ici.
Nota : tous les scripts de cette page sont des productions originales, réalisées dans un but pédagogique précis : allier facilement algorithme et langage de programmation. Aucune performance de programmation n'est recherchée, les scripts sont perfectibles. Cette page a pour vocation d'utiliser les TICE comme prétexte pour "faire des maths" ! Amusez-vous bien !
Collège
Thème :
Tracé de motifs géométriques générés aléatoirement sous Scratch.
Principe :
Problème inspiré du DNB 2022 - Amérique :
Visuel :
Téléchargement :
Seconde générale
Thème :
Arithmétique des entiers - Recherche de nombres premiers < N.
Principe :
On fait défiler tous les entiers de 2 à N, et pour chacun d'entre eux, on compte tous les diviseurs. On ne garde que les entiers qui ont uniquement 2 diviseurs (1 et eux-même, par la définition des nombres premiers)
Visuel :
Téléchargement :
Thème :
Arithmétique des entiers - Recherche des diviseurs d'un entier N.
Principe :
On fait défiler tous les entiers de 2 à N, et pour chacun d'entre eux, on vérifie s'ils divisent N ou non. On affiche les diviseurs et s'il n'y en a que 2, on dit que N est premier.
Visuel :
Téléchargement :
Thème :
Vecteurs du plan. Colinéarité dans un repère.
Principe :
On entre les coordonnées de 4 points du plan A, B, C, D. Le script calcule les coordonnées des vecteurs AB et CD, puis le déterminant de ces 2 vecteurs, conclut sur leur colinéarité et les trace sur un schéma repéré.
Visuel :
Téléchargement :
Première générale - Spé maths
Thème :
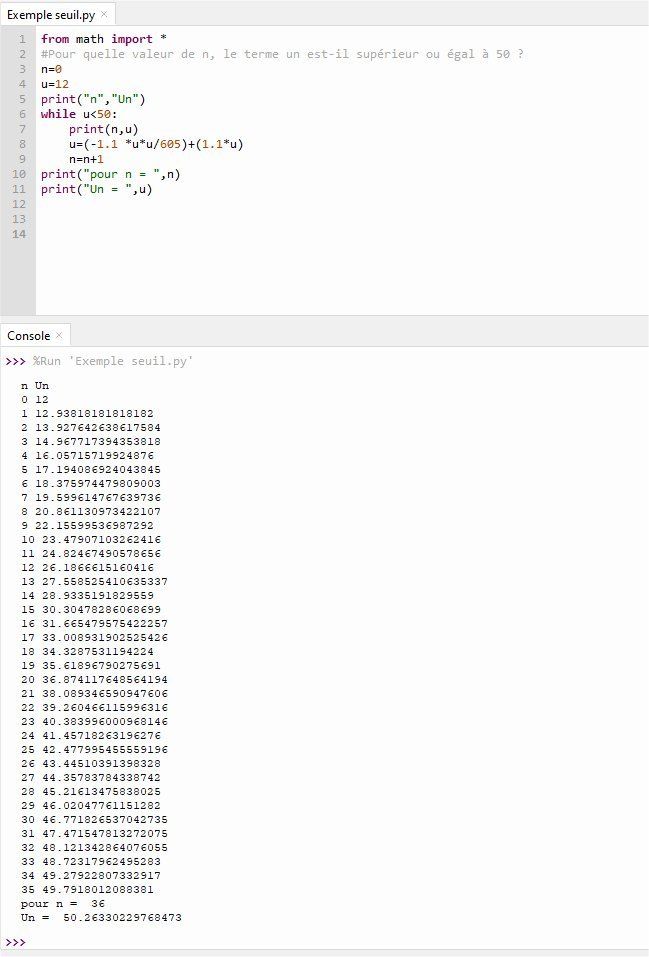
Suites numériques - Algorithme de seuil
Principe :
A partir de quel rang n, une suite numérique voit son terme Un supérieur (ou inférieur) à une valeur donnée ?
Exemple ici avec une suite croissante.
Visuel :
Téléchargement :
Terminale générale - Spé maths / maths complémentaires
Thème :
Primitives - tracé de la primitive d'une fonction ayant une valeur connue en un point - Méthode d'Euler
Principe :
Source : https://cassiopee.g-eau.fr/assets/docs/fr/methodes_numeriques/euler_explicite.html
Visuel :
Ex : tracé de la fonction ln à partir de f(x)=1/x et ln(1)=0
Téléchargement :
Thème :
Calcul intégral - approximation par la méthode des rectangles
Principe :
Cette méthode, très élémentaire, basée sur les sommes de Cauchy-Riemann (approchant l'aire sous une courbe) et appliquée à une fonction f continue, permet le calcul approché d'intégrales en choisissant une subdivision régulière de pas xi+1 - xi = (b - a)/n, donc indépendant de i avec une valeur de n "suffisamment grande". Le passage à la limite fournit l'intégrale cherchée.
Visuel :
Téléchargement :
Thème :
Fonctions numériques - Un outil d'étude complet
Principe :
Courbe représentative, dérivée, équation de tangente, recherche de racines, intégration par la méthode des rectangles ou par la méthode de Monté-Carlo, ...
Visuel :
Téléchargement :
Thème :
Probabilités et chaînes de Markov.
Les urnes d’Ehrenfest
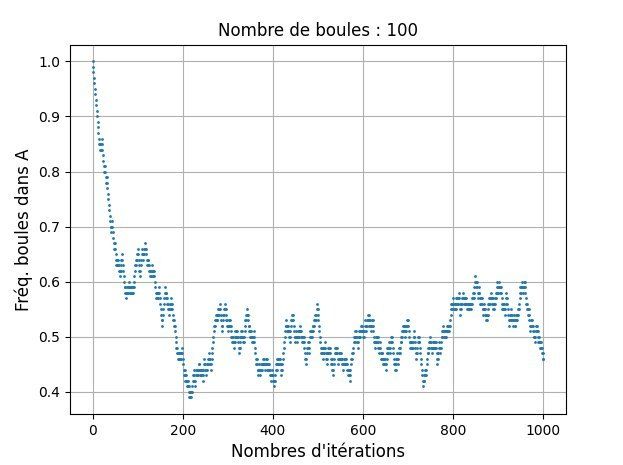
Principe :
Un nombre donné de boules numérotées sont initialement contenues dans une urne nommée A. On pioche aléatoirement un numéro de boule. Si la boule correspondante est dans A, on la met dans B. Une nouvelle pioche donnera une boule qui est soit dans A (probable au début), soit dans B. On dispose cette boule dans l'autre urne, et ainsi de suite...On analyse la proportion de boules dans A en fonction du nombre de tirages... Est-il possible qu'à un moment donné, 100% des boules reviennent dans A ? Et pour un grand nombre de tirages, cette proportion tend-elle vers une valeur limite ?
A étudier expérimentalement, conjectures à démontrer mathématiquement...
Visuel :
Téléchargement :
Thème :
Calcul d'aires.
Toutes méthodes autorisées !
Principe :
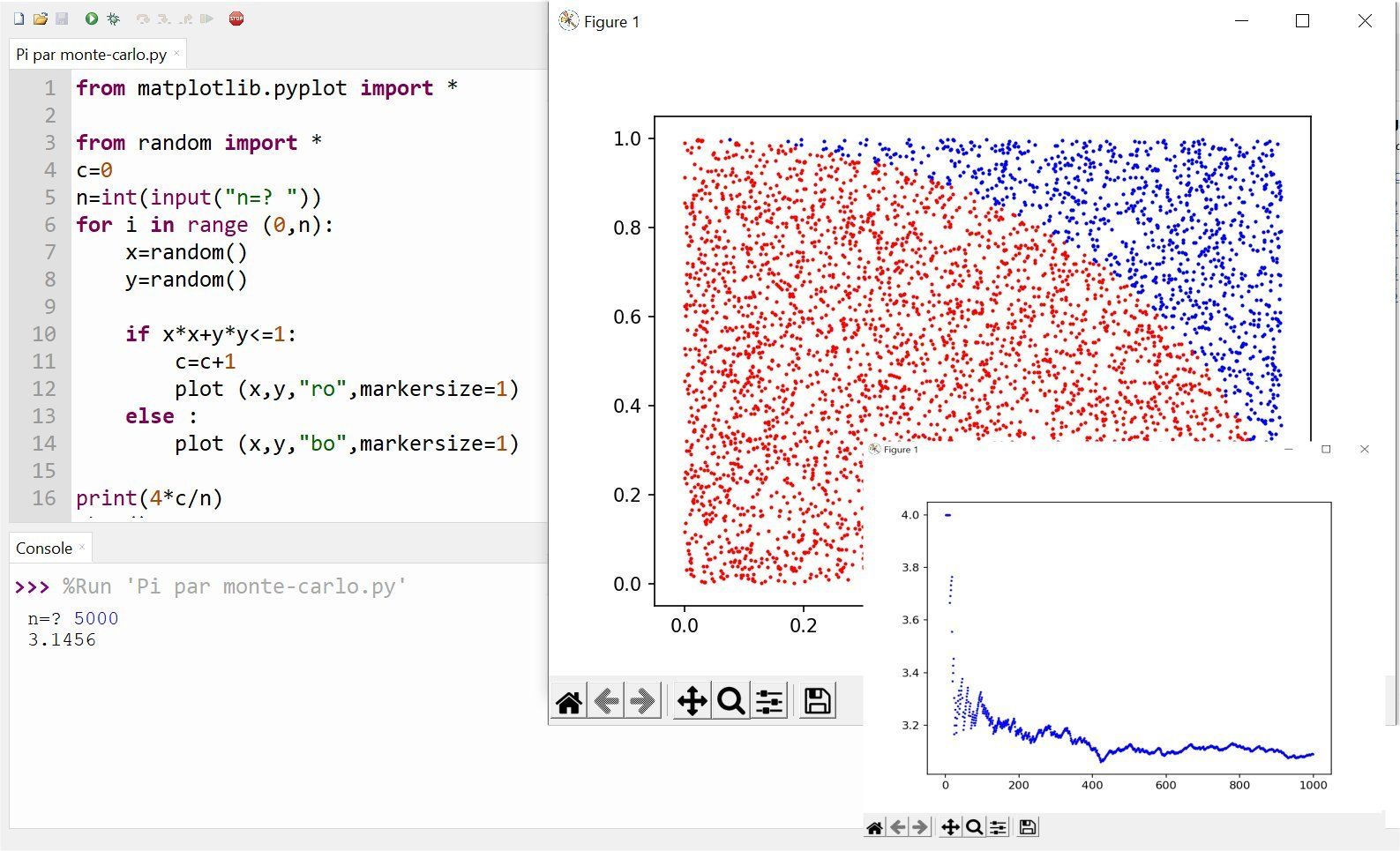
Il existe de nombreuses méthodes pour calculer des valeurs approchées d'aires : par le calcul intégral quand on connait l'expression des fonctions associées aux contours des aires à calculer, par la méthode de Monté-Carlo (approche probabiliste), par des méthodes de balayage, etc...
Un exercice inspiré d'une excellente activité créée par M. Jean-Philippe Blaise (Académie d'Amiens) : calculer l'aire de ce logo :
Des documents de travail sont disponibles : ici
Visuel :
CPGE - Ecoles d'ingénieurs - Licences
Thème :
Les coniques : ellipses
La gravitation universelle selon Newton
Principe :
A partir du principe fondamental de la dynamique et de la loi de gravitation universelle de Newton, il est possible de redémontrer les lois de Kepler, et en particulier de remarquer qu'un satellite tourne toujours sur une trajectoire elliptique autour de son astre principal.
A démontrer mathématiquement...
Et à illustrer avec Géogébra...
Visuel :
Téléchargement :
Thème :
Les développements limités
Principe :
Un développement limité (noté DL) d'une fonction en un point est une approximation polynomiale de cette fonction au voisinage de ce point, c'est-à-dire l'écriture de cette fonction sous la forme de la somme :
- d'une fonction polynomiale ;
- d'un reste négligeable au voisinage du point considéré.
Les développements limités permettent de trouver plus simplement des limites de fonctions, de calculer des dérivées, de prouver qu'une fonction est intégrable ou non, ou encore d'étudier des positions de courbes par rapport à des tangentes. Ils permettent également l'obtention d'équivalents.
Visuel :
Téléchargement :